Properties of ATOM.

Properties of ATOM.

 

Nuclear properties:~

By definition, any two atoms with an identical number of protons in their nuclei belong to the same chemical element. Atoms with equal numbers of protons but a different number of neutrons are different isotopes of the same element. For example, all hydrogen atoms admit exactly one proton, but isotopes exist with no neutrons (hydrogen-1, by far the most common form, also called protium), one neutron (deuterium), two neutrons (tritium) and more than two neutrons. The known elements form a set of atomic numbers, from the single proton element hydrogen up to the 118-proton element ununoctium. All known isotopes of elements with atomic numbers greater than 82 are radioactive.

About 339 nuclides occur naturally on Earth, of which 254 (about 75%) have not been observed to decay, and are referred to as "stable isotopes". However, only 90 of these nuclides are stable to all decay, even in theory. Another 164 (bringing the total to 254) have not been observed to decay, even though in theory it is energetically possible. These are also formally classified as "stable". An additional 34 radioactive nuclides have half-lives longer than 80 million years, and are long-lived enough to be present from the birth of the solar system. This collection of 288 nuclides are known as primordial nuclides. Finally, an additional 51 short-lived nuclides are known to occur naturally, as daughter products of primordial nuclide decay (such as radium from uranium), or else as products of natural energetic processes on Earth, such as cosmic ray bombardment (for example, carbon-14).

For 80 of the chemical elements, at least one stable isotope exists. As a rule, there is only a handful of stable isotopes for each of these elements, the average being 3.2 stable isotopes per element. Twenty-six elements have only a single stable isotope, while the largest number of stable isotopes observed for any element is ten, for the element tin. Elements 43, 61, and all elements numbered 83 or higher have no stable isotopes.

Stability of isotopes is affected by the ratio of protons to neutrons, and also by the presence of certain "magic numbers" of neutrons or protons that represent closed and filled quantum shells. These quantum shells correspond to a set of energy levels within the shell model of the nucleus; filled shells, such as the filled shell of 50 protons for tin, confers unusual stability on the nuclide. Of the 254 known stable nuclides, only four have both an odd number of protons and odd number of neutrons: hydrogen-2 (deuterium), lithium-6, boron-10 and nitrogen-14. Also, only four naturally occurring, radioactive odd–odd nuclides have a half-life over a billion years: potassium-40, vanadium-50, lanthanum-138 and tantalum-180m. Most odd–odd nuclei are highly unstable with respect to beta decay, because the decay products are even–even, and are therefore more strongly bound, due to nuclear pairing effects.

 

Mass.

The large majority of an atom's mass comes from the protons and neutrons that make it up. The total number of these particles (called "nucleons") in a given atom is called the mass number. It is a positive integer and dimensionless (instead of having dimension of mass), because it expresses a count. An example of use of a mass number is "carbon-12," which has 12 nucleons (six protons and six neutrons).

The actual mass of an atom at rest is often expressed using the unified atomic mass unit (u), also called dalton (Da). This unit is defined as a twelfth of the mass of a free neutral atom of carbon-12, which is approximately 1.66×10⁻²⁷ kg. Hydrogen-1 (the lightest isotope of hydrogen which is also the nuclide with the lowest mass) has an atomic weight of 1.007825 u. The value of this number is called the atomic mass. A given atom has an atomic mass approximately equal (within 1%) to its mass number times the atomic mass unit (for example the mass of a nitrogen-14 is roughly 14 u). However, this number will not be exactly an integer except in the case of carbon-12 (see below). The heaviest stable atom is lead-208, with a mass of 207.9766521 u.

As even the most massive atoms are far too light to work with directly, chemists instead use the unit of moles. One mole of atoms of any element always has the same number of atoms (about 6.022×10²³). This number was chosen so that if an element has an atomic mass of 1 u, a mole of atoms of that element has a mass close to one gram. Because of the definition of the unified atomic mass unit, each carbon-12 atom has an atomic mass of exactly 12 u, and so a mole of carbon-12 atoms weighs exactly 0.012 kg.

 

 

Shape and size:~

Atoms lack a well-defined outer boundary, so their dimensions are usually described in terms of an atomic radius. This is a measure of the distance out to which the electron cloud extends from the nucleus. However, this assumes the atom to exhibit a spherical shape, which is only obeyed for atoms in vacuum or free space. Atomic radii may be derived from the distances between two nuclei when the two atoms are joined in a chemical bond. The radius varies with the location of an atom on the atomic chart, the type of chemical bond, the number of neighboring atoms (coordination number) and a quantum mechanical property known as spin. On the periodic table of the elements, atom size tends to increase when moving down columns, but decrease when moving across rows (left to right). Consequently, the smallest atom is helium with a radius of 32 pm, while one of the largest is caesium at 225 pm.

When subjected to external forces, like electrical fields, the shape of an atom may deviate from spherical symmetry. The deformation depends on the field magnitude and the orbital type of outer shell electrons, as shown by group-theoretical considerations. Aspherical deviations might be elicited for instance in crystals, where large crystal-electrical fields may occur at low-symmetry lattice sites. Significant ellipsoidal deformations have recently been shown to occur for sulfur ions and chalcogen ions in pyrite-type compounds.

Atomic dimensions are thousands of times smaller than the wavelengths of light (400–700 nm) so they cannot be viewed using an optical microscope. However, individual atoms can be observed using a scanning tunneling microscope. To visualize the minuteness of the atom, consider that a typical human hair is about 1 million carbon atoms in width. A single drop of water contains about 2 sextillion (2×10²¹) atoms of oxygen, and twice the number of hydrogen atoms. A single carat diamond with a mass of 2×10⁻⁴ kg contains about 10 sextillion (10²²) atoms of carbon. If an apple were magnified to the size of the Earth, then the atoms in the apple would be approximately the size of the original apple.

Radioactive decay.

This diagram shows the half-life (T_½) of various isotopes with Z protons and N neutrons.

Every element has one or more isotopes that have unstable nuclei that are subject to radioactive decay, causing the nucleus to emit particles or electromagnetic radiation. Radioactivity can occur when the radius of a nucleus is large compared with the radius of the strong force, which only acts over distances on the order of 1 fm.

• Alpha decay: this process is caused when the nucleus emits an alpha particle, which is a helium nucleus consisting of two protons and two neutrons. The result of the emission is a new element with a lower atomic number.
• Beta decay (and electron capture): these processes are regulated by the weak force, and result from a transformation of a neutron into a proton, or a proton into a neutron. The neutron to proton transition is accompanied by the emission of an electron and an antineutrino, while proton to neutron transition (except in electron capture) causes the emission of a positron and a neutrino. The electron or positron emissions are called beta particles. Beta decay either increases or decreases the atomic number of the nucleus by one. Electron capture is more common than positron emission, because it requires less energy. In this type of decay, an electron is absorbed by the nucleus, rather than a positron emitted from the nucleus. A neutrino is still emitted in this process, and a proton changes to a neutron.
• Gamma decay: this process results from a change in the energy level of the nucleus to a lower state, resulting in the emission of electromagnetic radiation. The excited state of a nucleus which results in gamma emission usually occurs following the emission of an alpha or a beta particle. Thus, gamma decay usually follows alpha or beta decay.

Other more rare types of radioactive decay include ejection of neutrons or protons or clusters of nucleons from a nucleus, or more than one beta particle. An analog of gamma emission which allows excited nuclei to lose energy in a different way, is internal conversion— a process that produces high-speed electrons that are not beta rays, followed by production of high-energy photons that are not gamma rays. A few large nuclei explode into two or more charged fragments of varying masses plus several neutrons, in a decay called spontaneous nuclear fission.

Each radioactive isotope has a characteristic decay time period—the half-life—that is determined by the amount of time needed for half of a sample to decay. This is an exponential decay process that steadily decreases the proportion of the remaining isotope by 50% every half-life. Hence after two half-lives have passed only 25% of the isotope is present, and so forth.

 

 

Magnetic moment.

Elementary particles possess an intrinsic quantum mechanical property known as spin. This is analogous to the angular momentum of an object that is spinning around its center of mass, although strictly speaking these particles are believed to be point-like and cannot be said to be rotating. Spin is measured in units of the reduced Planck constant (ħ), with electrons, protons and neutrons all having spin ½ ħ, or "spin-½". In an atom, electrons in motion around the nucleus possess orbital angular momentum in addition to their spin, while the nucleus itself possesses angular momentum due to its nuclear spin.

The magnetic field produced by an atom—its magnetic moment—is determined by these various forms of angular momentum, just as a rotating charged object classically produces a magnetic field. However, the most dominant contribution comes from electron spin. Due to the nature of electrons to obey the Pauli exclusion principle, in which no two electrons may be found in the same quantum state, bound electrons pair up with each other, with one member of each pair in a spin up state and the other in the opposite, spin down state. Thus these spins cancel each other out, reducing the total magnetic dipole moment to zero in some atoms with even number of electrons.
 
In ferromagnetic elements such as iron, cobalt and nickel, an odd number of electrons leads to an unpaired electron and a net overall magnetic moment. The orbitals of neighboring atoms overlap and a lower energy state is achieved when the spins of unpaired electrons are aligned with each other, a spontaneous process known as an exchange interaction. When the magnetic moments of ferromagnetic atoms are lined up, the material can produce a measurable macroscopic field. Paramagnetic materials have atoms with magnetic moments that line up in random directions when no magnetic field is present, but the magnetic moments of the individual atoms line up in the presence of a field.

The nucleus of an atom will have no spin when it has even numbers of both neutrons and protons, but for other cases of odd numbers, the nucleus may have a spin. Normally nuclei with spin are aligned in random directions because of thermal equilibrium. However, for certain elements (such as xenon-129) it is possible to polarize a significant proportion of the nuclear spin states so that they are aligned in the same direction—a condition called hyperpolarization. This has important applications in magnetic resonance imaging.

 

 

Energy levels.

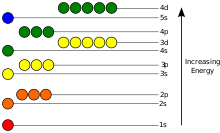These electron's energy levels (not to scale) are sufficient for ground states of atoms up to cadmium (5s² 4d¹⁰) inclusively. Do not forget that even the top of the diagram is lower than an unbound electron state.

The potential energy of an electron in an atom is negative, its dependence of its position reaches the minimum (the most absolute value) inside the nucleus, and vanishes when the distance from the nucleus goes to infinity, roughly in an inverse proportion to the distance. In the quantum-mechanical model, a bound electron can only occupy a set of states centered on the nucleus, and each state corresponds to a specific energy level; see time-independent Schrödinger equation for theoretical explanation. An energy level can be measured by the amount of energy needed to unbind the electron from the atom, and is usually given in units of electronvolts (eV). The lowest energy state of a bound electron is called the ground state, i.e. stationary state, while an electron transition to a higher level results in an excited state. The electron's energy raises when n increases because the (average) distance to the nucleus increases. Dependence of the energy on ℓ is caused not by electrostatic potential of the nucleus, but by interaction between electrons.

For an electron to transition between two different states, e.g. grounded state to first excited level (ionization), it must absorb or emit a photon at an energy matching the difference in the potential energy of those levels, according to Niels Bohr model, what can be precisely calculated by the Schrödinger equation. Electrons jump between orbitals in a particle-like fashion. For example, if a single photon strikes the electrons, only a single electron changes states in response to the photon; see Electron properties.

The energy of an emitted photon is proportional to its frequency, so these specific energy levels appear as distinct bands in the electromagnetic spectrum. Each element has a characteristic spectrum that can depend on the nuclear charge, subshells filled by electrons, the electromagnetic interactions between the electrons and other factors.

An example of absorption lines in a spectrum

When a continuous spectrum of energy is passed through a gas or plasma, some of the photons are absorbed by atoms, causing electrons to change their energy level. Those excited electrons that remain bound to their atom spontaneously emit this energy as a photon, traveling in a random direction, and so drop back to lower energy levels. Thus the atoms behave like a filter that forms a series of dark absorption bands in the energy output. (An observer viewing the atoms from a view that does not include the continuous spectrum in the background, instead sees a series of emission lines from the photons emitted by the atoms.) Spectroscopic measurements of the strength and width of atomic spectral lines allow the composition and physical properties of a substance to be determined.

Close examination of the spectral lines reveals that some display a fine structure splitting. This occurs because of spin–orbit coupling, which is an interaction between the spin and motion of the outermost electron. When an atom is in an external magnetic field, spectral lines become split into three or more components; a phenomenon called the Zeeman effect. This is caused by the interaction of the magnetic field with the magnetic moment of the atom and its electrons. Some atoms can have multiple electron configurations with the same energy level, which thus appear as a single spectral line. The interaction of the magnetic field with the atom shifts these electron configurations to slightly different energy levels, resulting in multiple spectral lines. The presence of an external electric field can cause a comparable splitting and shifting of spectral lines by modifying the electron energy levels, a phenomenon called the Stark effect.

If a bound electron is in an excited state, an interacting photon with the proper energy can cause stimulated emission of a photon with a matching energy level. For this to occur, the electron must drop to a lower energy state that has an energy difference matching the energy of the interacting photon. The emitted photon and the interacting photon then move off in parallel and with matching phases. That is, the wave patterns of the two photons are synchronized. This physical property is used to make lasers, which can emit a coherent beam of light energy in a narrow frequency band.

 

 

Valence and bonding behavior.

Valency is the combining power of an element. It is equal to number of hydrogen atoms that atom can combine or displace in forming compounds. The outermost electron shell of an atom in its uncombined state is known as the valence shell, and the electrons in that shell are called valence electrons. The number of valence electrons determines the bonding behavior with other atoms. Atoms tend to chemically react with each other in a manner that fills (or empties) their outer valence shells. For example, a transfer of a single electron between atoms is a useful approximation for bonds that form between atoms with one-electron more than a filled shell, and others that are one-electron short of a full shell, such as occurs in the compound sodium chloride and other chemical ionic salts. However, many elements display multiple valences, or tendencies to share differing numbers of electrons in different compounds. Thus, chemical bonding between these elements takes many forms of electron-sharing that are more than simple electron transfers. Examples include the element carbon and the organic compounds.

The chemical elements are often displayed in a periodic table that is laid out to display recurring chemical properties, and elements with the same number of valence electrons form a group that is aligned in the same column of the table. (The horizontal rows correspond to the filling of a quantum shell of electrons.) The elements at the far right of the table have their outer shell completely filled with electrons, which results in chemically inert elements known as the noble gases.

 

 

States.

Snapshots illustrating the formation of a Bose–Einstein condensate

Quantities of atoms are found in different states of matter that depend on the physical conditions, such as temperature and pressure. By varying the conditions, materials can transition between solids, liquids, gases and plasmas. Within a state, a material can also exist in different allotropes. An example of this is solid carbon, which can exist as graphite or diamond. Gaseous allotropes exist as well, such as dioxygen and ozone.

At temperatures close to absolute zero, atoms can form a Bose–Einstein condensate, at which point quantum mechanical effects, which are normally only observed at the atomic scale, become apparent on a macroscopic scale. This super-cooled collection of atoms then behaves as a single super atom, which may allow fundamental checks of quantum mechanical behavior.

Atom.

An atom is the smallest constituent unit of ordinary matter that has the properties of a chemical element. Every solid, liquid, gas, and plasma is composed of neutral or ionized atoms. Atoms are very small; typical sizes are around 100 pm (a ten-billionth of a meter, in the short scale). However, atoms do not have well-defined boundaries, and there are different ways to define their size that give different but close values.

Atoms are small enough that attempting to predict their behavior using classical physics - as if they were billiard balls, for example - gives noticeably incorrect predictions due to quantum effects. Through the development of physics, atomic models have incorporated quantum principles to better explain and predict the behavior.

Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and typically a similar number of neutrons. Protons and neutrons are called nucleons. More than 99.94% of an atom's mass is in the nucleus. The protons have a positive electric charge, the electrons have a negative electric charge, and the neutrons have no electric charge. If the number of protons and electrons are equal, that atom is electrically neutral. If an atom has more or fewer electrons than protons, then it has an overall negative or positive charge, respectively, and it is called an ion.

The electrons of an atom are attracted to the protons in an atomic nucleus by this electromagnetic force. The protons and neutrons in the nucleus are attracted to each other by a different force, the nuclear force, which is usually stronger than the electromagnetic force repelling the positively charged protons from one another. Under certain circumstances the repelling electromagnetic force becomes stronger than the nuclear force, and nucleons can be ejected from the nucleus, leaving behind a different element: nuclear decay resulting in nuclear transmutation.

The number of protons in the nucleus defines to what chemical element the atom belongs: for example, all copper atoms contain 29 protons. The number of neutrons defines the isotope of the element. The number of electrons influences the magnetic properties of an atom. Atoms can attach to one or more other atoms by chemical bonds to form chemical compounds such as molecules. The ability of atoms to associate and dissociate is responsible for most of the physical changes observed in nature, and is the subject of the discipline of chemistry.

 

History of atomic theory.

 

Atoms in philosophy:~

The idea that matter is made up of discrete units is a very old idea, appearing in many ancient cultures such as Greece and India. The word "atom" was coined by ancient Greek philosophers. However, these ideas were founded in philosophical and theological reasoning rather than evidence and experimentation. As a result, their views on what atoms look like and how they behave were incorrect. They also could not convince everybody, so atomism was but one of a number of competing theories on the nature of matter. It was not until the 19th century that the idea was embraced and refined by scientists, when the blossoming science of chemistry produced discoveries that only the concept of atoms could explain.

 

 

First evidence-based theory:~

Various atoms and molecules as depicted in John Dalton's A New System of Chemical Philosophy (1808).

In the early 1800s, John Dalton used the concept of atoms to explain why elements always react in ratios of small whole numbers (the law of multiple proportions). For instance, there are two types of tin oxide: one is 88.1% tin and 11.9% oxygen and the other is 78.7% tin and 21.3% oxygen (tin(II) oxide and tin dioxide respectively). This means that 100g of tin will combine either with 13.5g or 27g of oxygen. 13.5 and 27 form a ratio of 1:2, a ratio of small whole numbers. This common pattern in chemistry suggested to Dalton that elements react in whole number multiples of discrete units—in other words, atoms. In the case of tin oxides, one tin atom will combine with either one or two oxygen atoms.

Dalton also believed atomic theory could explain why water absorbs different gases in different proportions. For example, he found that water absorbs carbon dioxide far better than it absorbs nitrogen. Dalton hypothesized this was due to the differences between the masses and configurations of the gases' respective particles, and carbon dioxide molecules (CO₂) are heavier and larger than nitrogen molecules (N₂).

 

 

Brownian motion:~

In 1827, botanist Robert Brown used a microscope to look at dust grains floating in water and discovered that they moved about erratically, a phenomenon that became known as "Brownian motion". This was thought to be caused by water molecules knocking the grains about. In 1905 Albert Einstein proved the reality of these molecules and their motions by producing the first Statistical physics analysis of Brownian motion. French physicist Jean Perrin used Einstein's work to experimentally determine the mass and dimensions of atoms, thereby conclusively verifying Dalton's atomic theory.

 

Discovery of the electron.

 

The Geiger–Marsden experiment
Top: Expected results: alpha particles passing through the plum pudding model of the atom with negligible deflection.
Bottom: Observed results: a small portion of the particles were deflected by the concentrated positive charge of the nucleus.

The physicist J. J. Thomson measured the mass of cathode rays, showing they were made of particles, but were around 1800 times lighter than the lightest atom, hydrogen. Therefore, they were not atoms, but a new particle, the first subatomic particle to be discovered, which he originally called "corpuscle" but was later named electron, after particles postulated by George Johnstone Stoney in 1874. He also showed they were identical to particles given off by photoelectric and radioactive materials. It was quickly recognized that they are the particles that carry electric currents in metal wires, and carry the negative electric charge within atoms. Thomson was given the 1906 Nobel Prize in Physics for this work. Thus he overturned the belief that atoms are the indivisible, ultimate particles of matter. Thomson also incorrectly postulated that the low mass, negatively charged electrons were distributed throughout the atom in a uniform sea of positive charge. This became known as the plum pudding model.

 

 

Discovery of the nucleus.

 

In 1909, Hans Geiger and Ernest Marsden, under the direction of Ernest Rutherford, bombarded a metal foil with alpha particles to observe how they scattered. They expected all the alpha particles to pass straight through with little deflection, because Thomson's model said that the charges in the atom are so diffuse that their electric fields could not affect the alpha particles much. However, Geiger and Marsden spotted alpha particles being deflected by angles greater than 90°, which was supposed to be impossible according to Thomson's model. To explain this, Rutherford proposed that the positive charge of the atom is concentrated in a tiny nucleus at the center of the atom.

 

Discovery of isotopes.

While experimenting with the products of radioactive decay, in 1913 radiochemist Frederick Soddy discovered that there appeared to be more than one type of atom at each position on the periodic table. The term isotope was coined by Margaret Todd as a suitable name for different atoms that belong to the same element. J.J. Thomson created a technique for separating atom types through his work on ionized gases, which subsequently led to the discovery of stable isotopes.

 

 

Bohr model.

 

The Bohr model of the atom, with an electron making instantaneous "quantum leaps" from one orbit to another. This model is obsolete.

In 1913 the physicist Niels Bohr proposed a model in which the electrons of an atom were assumed to orbit the nucleus but could only do so in a finite set of orbits, and could jump between these orbits only in discrete changes of energy corresponding to absorption or radiation of a photon. This quantization was used to explain why the electrons orbits are stable (given that normally, charges in acceleration, including circular motion, lose kinetic energy which is emitted as electromagnetic radiation, see synchrotron radiation) and why elements absorb and emit electromagnetic radiation in discrete spectra.

Later in the same year Henry Moseley provided additional experimental evidence in favor of Niels Bohr's theory. These results refined Ernest Rutherford's and Antonius Van den Broek's model, which proposed that the atom contains in its nucleus a number of positive nuclear charges that is equal to its (atomic) number in the periodic table. Until these experiments, atomic number was not known to be a physical and experimental quantity. That it is equal to the atomic nuclear charge remains the accepted atomic model today.

 

 

Chemical bonding explained:~

Chemical bonds between atoms were now explained, by Gilbert Newton Lewis in 1916, as the interactions between their constituent electrons. As the chemical properties of the elements were known to largely repeat themselves according to the periodic law, in 1919 the American chemist Irving Langmuir suggested that this could be explained if the electrons in an atom were connected or clustered in some manner. Groups of electrons were thought to occupy a set of electron shells about the nucleus.

 

 

Further developments in quantum physics.

The Stern–Gerlach experiment of 1922 provided further evidence of the quantum nature of the atom. When a beam of silver atoms was passed through a specially shaped magnetic field, the beam was split based on the direction of an atom's angular momentum, or spin. As this direction is random, the beam could be expected to spread into a line. Instead, the beam was split into two parts, depending on whether the atomic spin was oriented up or down.

In 1924, Louis de Broglie proposed that all particles behave to an extent like waves. In 1926, Erwin Schrödinger used this idea to develop a mathematical model of the atom that described the electrons as three-dimensional waveforms rather than point particles. A consequence of using waveforms to describe particles is that it is mathematically impossible to obtain precise values for both the position and momentum of a particle at a given point in time; this became known as the uncertainty principle, formulated by Werner Heisenberg in 1926. In this concept, for a given accuracy in measuring a position one could only obtain a range of probable values for momentum, and vice versa. This model was able to explain observations of atomic behavior that previous models could not, such as certain structural and spectral patterns of atoms larger than hydrogen. Thus, the planetary model of the atom was discarded in favor of one that described atomic orbital zones around the nucleus where a given electron is most likely to be observed.

 

 

Discovery of the neutron.

The development of the mass spectrometer allowed the mass of atoms to be measured with increased accuracy. The device uses a magnet to bend the trajectory of a beam of ions, and the amount of deflection is determined by the ratio of an atom's mass to its charge. The chemist Francis William Aston used this instrument to show that isotopes had different masses. The atomic mass of these isotopes varied by integer amounts, called the whole number rule. The explanation for these different isotopes awaited the discovery of the neutron, an uncharged particle with a mass similar to the proton, by the physicist James Chadwick in 1932. Isotopes were then explained as elements with the same number of protons, but different numbers of neutrons within the nucleus.

 

 

Fission, high-energy physics and condensed matter.

In 1938, the German chemist Otto Hahn, a student of Rutherford, directed neutrons onto uranium atoms expecting to get transuranium elements. Instead, his chemical experiments showed barium as a product. A year later, Lise Meitner and her nephew Otto Frisch verified that Hahn's result were the first experimental nuclear fission. In 1944, Hahn received the Nobel prize in chemistry. Despite Hahn's efforts, the contributions of Meitner and Frisch were not recognized.

In the 1950s, the development of improved particle accelerators and particle detectors allowed scientists to study the impacts of atoms moving at high energies. Neutrons and protons were found to be hadrons, or composites of smaller particles called quarks. The standard model of particle physics was developed that so far has successfully explained the properties of the nucleus in terms of these sub-atomic particles and the forces that govern their interactions.

 

 

Structure.

Subatomic particles:~

Though the word atom originally denoted a particle that cannot be cut into smaller particles, in modern scientific usage the atom is composed of various subatomic particles. The constituent particles of an atom are the electron, the proton and the neutron; all three are fermions. However, the hydrogen-1 atom has no neutrons and the hydron ion has no electrons.

The electron is by far the least massive of these particles at 9.11×10⁻³¹ kg, with a negative electrical charge and a size that is too small to be measured using available techniques. It is the lightest particle with a positive rest mass measured. Under ordinary conditions, electrons are bound to the positively charged nucleus by the attraction created from opposite electric charges. If an atom has more or fewer electrons than its atomic number, then it becomes respectively negatively or positively charged as a whole; a charged atom is called an ion. Electrons have been known since the late 19th century, mostly thanks to J.J. Thomson; see history of subatomic physics for details.

Protons have a positive charge and a mass 1,836 times that of the electron, at 1.6726×10⁻²⁷ kg. The number of protons in an atom is called its atomic number. Ernest Rutherford (1919) observed that nitrogen under alpha-particle bombardment ejects what appeared to be hydrogen nuclei. By 1920 he had accepted that the hydrogen nucleus is a distinct particle within the atom and named it proton.

Neutrons have no electrical charge and have a free mass of 1,839 times the mass of the electron, or 1.6929×10⁻²⁷ kg, the heaviest of the three constituent particles, but it can be reduced by the nuclear binding energy. Neutrons and protons (collectively known as nucleons) have comparable dimensions—on the order of 2.5×10⁻¹⁵ m—although the 'surface' of these particles is not sharply defined. The neutron was discovered in 1932 by the English physicist James Chadwick.

In the Standard Model of physics, electrons are truly elementary particles with no internal structure. However, both protons and neutrons are composite particles composed of elementary particles called quarks. There are two types of quarks in atoms, each having a fractional electric charge. Protons are composed of two up quarks (each with charge +2/3) and one down quark (with a charge of −1/3). Neutrons consist of one up quark and two down quarks. This distinction accounts for the difference in mass and charge between the two particles.

The quarks are held together by the strong interaction (or strong force), which is mediated by gluons. The protons and neutrons, in turn, are held to each other in the nucleus by the nuclear force, which is a residuum of the strong force that has somewhat different range-properties (see the article on the nuclear force for more). The gluon is a member of the family of gauge bosons, which are elementary particles that mediate physical forces.

 

 

Nucleus.

The binding energy needed for a nucleon to escape the nucleus, for various isotopes

All the bound protons and neutrons in an atom make up a tiny atomic nucleus, and are collectively called nucleons. The radius of a nucleus is approximately equal to 1.07 ³√A fm, where A is the total number of nucleons. This is much smaller than the radius of the atom, which is on the order of 10⁵ fm. The nucleons are bound together by a short-ranged attractive potential called the residual strong force. At distances smaller than 2.5 fm this force is much more powerful than the electrostatic force that causes positively charged protons to repel each other.
 
Atoms of the same element have the same number of protons, called the atomic number. Within a single element, the number of neutrons may vary, determining the isotope of that element. The total number of protons and neutrons determine the nuclide. The number of neutrons relative to the protons determines the stability of the nucleus, with certain isotopes undergoing radioactive decay.

The proton, the electron, and the neutron are classified as fermions. Fermions obey the Pauli exclusion principle which prohibits identical fermions, such as multiple protons, from occupying the same quantum state at the same time. Thus, every proton in the nucleus must occupy a quantum state different from all other protons, and the same applies to all neutrons of the nucleus and to all electrons of the electron cloud. However, a proton and a neutron are allowed to occupy the same quantum state.

For atoms with low atomic numbers, a nucleus that has more neutrons than protons tends to drop to a lower energy state through radioactive decay so that the neutron–proton ratio is closer to one. However, as the atomic number increases, a higher proportion of neutrons is required to offset the mutual repulsion of the protons. Thus, there are no stable nuclei with equal proton and neutron numbers above atomic number Z = 20 (calcium) and as Z increases, the neutron–proton ratio of stable isotopes increases. The stable isotope with the highest proton–neutron ratio is lead-208 (about 1.5).

Illustration of a nuclear fusion process that forms a deuterium nucleus, consisting of a proton and a neutron, from two protons. A positron (e⁺)—an antimatter electron—is emitted along with an electron neutrino.

The number of protons and neutrons in the atomic nucleus can be modified, although this can require very high energies because of the strong force. Nuclear fusion occurs when multiple atomic particles join to form a heavier nucleus, such as through the energetic collision of two nuclei. For example, at the core of the Sun protons require energies of 3–10 keV to overcome their mutual repulsion—the coulomb barrier—and fuse together into a single nucleus. Nuclear fission is the opposite process, causing a nucleus to split into two smaller nuclei—usually through radioactive decay. The nucleus can also be modified through bombardment by high energy subatomic particles or photons. If this modifies the number of protons in a nucleus, the atom changes to a different chemical element.

If the mass of the nucleus following a fusion reaction is less than the sum of the masses of the separate particles, then the difference between these two values can be emitted as a type of usable energy (such as a gamma ray, or the kinetic energy of a beta particle), as described by Albert Einstein's mass–energy equivalence formula, E = mc², where m is the mass loss and c is the speed of light. This deficit is part of the binding energy of the new nucleus, and it is the non-recoverable loss of the energy that causes the fused particles to remain together in a state that requires this energy to separate.

The fusion of two nuclei that create larger nuclei with lower atomic numbers than iron and nickel—a total nucleon number of about 60—is usually an exothermic process that releases more energy than is required to bring them together. It is this energy-releasing process that makes nuclear fusion in stars a self-sustaining reaction. For heavier nuclei, the binding energy per nucleon in the nucleus begins to decrease. That means fusion processes producing nuclei that have atomic numbers higher than about 26, and atomic masses higher than about 60, is an endothermic process. These more massive nuclei can not undergo an energy-producing fusion reaction that can sustain the hydrostatic equilibrium of a star.

 

 

Electron cloud.

 

A potential well, showing, according to classical mechanics, the minimum energy V(x) needed to reach each position x. Classically, a particle with energy E is constrained to a range of positions between x₁ and x₂.

The electrons in an atom are attracted to the protons in the nucleus by the electromagnetic force. This force binds the electrons inside an electrostatic potential well surrounding the smaller nucleus, which means that an external source of energy is needed for the electron to escape. The closer an electron is to the nucleus, the greater the attractive force. Hence electrons bound near the center of the potential well require more energy to escape than those at greater separations.

Electrons, like other particles, have properties of both a particle and a wave. The electron cloud is a region inside the potential well where each electron forms a type of three-dimensional standing wave—a wave form that does not move relative to the nucleus. This behavior is defined by an atomic orbital, a mathematical function that characterises the probability that an electron appears to be at a particular location when its position is measured. Only a discrete (or quantized) set of these orbitals exist around the nucleus, as other possible wave patterns rapidly decay into a more stable form. Orbitals can have one or more ring or node structures, and differ from each other in size, shape and orientation.

Wave functions of the first five atomic orbitals. The three 2p orbitals each display a single angular node that has an orientation and a minimum at the center.

Each atomic orbital corresponds to a particular energy level of the electron. The electron can change its state to a higher energy level by absorbing a photon with sufficient energy to boost it into the new quantum state. Likewise, through spontaneous emission, an electron in a higher energy state can drop to a lower energy state while radiating the excess energy as a photon. These characteristic energy values, defined by the differences in the energies of the quantum states, are responsible for atomic spectral lines.

The amount of energy needed to remove or add an electron—the electron binding energy—is far less than the binding energy of nucleons. For example, it requires only 13.6 eV to strip a ground-state electron from a hydrogen atom, compared to 2.23 million eV for splitting a deuterium nucleus. Atoms are electrically neutral if they have an equal number of protons and electrons. Atoms that have either a deficit or a surplus of electrons are called ions. Electrons that are farthest from the nucleus may be transferred to other nearby atoms or shared between atoms. By this mechanism, atoms are able to bond into molecules and other types of chemical compounds like ionic and covalent network crystals.

Wormhole.

Wormholes by Rishabh Sharma on Scribd

A wormhole or "Einstein-Rosen Bridge" is a hypothetical topological feature that would fundamentally be a shortcut connecting two separate points in spacetime. A wormhole may connect extremely long distances such as a billion light years or more, short distances such as a few feet, different universes, and different points in time. A wormhole is much like a tunnel with two ends, each at separate points in spacetime.

For a simplified notion of a wormhole, space can be visualized as a two-dimensional (2D) surface. In this case, a wormhole would appear as a hole in that surface, lead into a 3D tube (the inside surface of a cylinder), then re-emerge at another location on the 2D surface with a hole similar to the entrance. An actual wormhole would be analogous to this, but with the spatial dimensions raised by one. For example, instead of circular holes on a 2D plane, the entry and exit points could be visualized as spheres in 3D space

Overview:~

The equations of the theory of general relativity have valid solutions that contain wormholes. The first type of wormhole solution discovered was the Schwarzschild wormhole, which would be present in the Schwarzschild metric describing an eternal black hole, but it was found that it would collapse too quickly for anything to cross from one end to the other. Wormholes that could be crossed in both directions, known as traversable wormholes, would only be possible if exotic matter with negative energy density could be used to stabilize them. Wormholes are also a very powerful mathematical metaphor for teaching general relativity.

The Casimir effect shows that quantum field theory allows the energy density in certain regions of space to be negative relative to the ordinary vacuum energy, and it has been shown theoretically that quantum field theory allows states where energy can be arbitrarily negative at a given point. Many physicists, such as Stephen Hawking, Kip Thorne and others, therefore argue that such effects might make it possible to stabilize a traversable wormhole. Physicists have not found any natural process that would be predicted to form a wormhole naturally in the context of general relativity, although the quantum foam hypothesis is sometimes used to suggest that tiny wormholes might appear and disappear spontaneously at the Planck scale, and stable versions of such wormholes have been suggested as dark matter candidates. It has also been proposed that, if a tiny wormhole held open by a negative mass cosmic string had appeared around the time of the Big Bang, it could have been inflated to macroscopic size by cosmic inflation.

The American theoretical physicist John Archibald Wheeler coined the term wormhole in 1957; the German mathematician Hermann Weyl, however, had proposed the wormhole theory in 1921, in connection with mass analysis of electromagnetic field energy.

This analysis forces one to consider situations... where there is a net flux of lines of force, through what topologists would call "a handle" of the multiply-connected space, and what physicists might perhaps be excused for more vividly terming a "wormhole".

— John Wheeler in Annals of Physics

"Embedding diagram" of a Schwarzschild wormhole

 

 

Definitions.

 

Topological:~

An intra-universe wormhole is a compact region of spacetime whose boundary is topologically trivial, but whose interior is not simply connected. Formalizing this idea leads to definitions such as the following, taken from Matt Visser's Lorentzian Wormholes.

If a Minkowski spacetime contains a compact region Ω, and if the topology of Ω is of the form Ω ~ R × Σ, where Σ is a three-manifold of the nontrivial topology, whose boundary has topology of the form ∂Σ ~ S², and if, furthermore, the hypersurfaces Σ are all spacelike, then the region Ω contains a quasipermanent intrauniverse wormhole.

   

 

Geometric:~

Wormholes have been defined geometrically, as opposed to topologically, as regions of spacetime that constrain the incremental deformation of closed surfaces. For example, in Enrico Rodrigo's The Physics of Stargates, a wormhole is defined informally as:

a region of spacetime containing a "world tube" (the time evolution of a closed surface) that cannot be continuously deformed (shrunk) to a world line (the time evolution of a point).

 

Schwarzschild wormholes.

An artist's impression of a wormhole from an observer's perspective, crossing the event horizon of a Schwarzschild wormhole that bridges two different universes. The observer originates from the right, and another universe becomes visible in the center of the wormhole's shadow once the horizon is crossed, the observer seeing light that has fallen into the black hole interior region from the other universe; however, this other universe is unreachable in the case of a Schwarzschild wormhole, as the bridge always collapses before the observer has time to cross it, and everything that has fallen through the event horizon of either universe is inevitably crushed in the singularity.

Lorentzian wormholes known as Schwarzschild wormholes or Einstein–Rosen bridges are connections between areas of space that can be modeled as vacuum solutions to the Einstein field equations, and that are now understood to be intrinsic parts of the maximally extended version of the Schwarzschild metric describing an eternal black hole with no charge and no rotation. Here, "maximally extended" refers to the idea that the space-time should not have any "edges": it should be possible to continue this path arbitrarily far into the particle's future or past for any possible trajectory of a free-falling particle (following a Geodesic in the spacetime), unless the trajectory hits a gravitational singularity like the one at the center of the black hole's interior.

In order to satisfy this requirement, it turns out that in addition to the black hole interior region that particles enter when they fall through the event horizon from the outside, there must be a separate white hole interior region that allows us to extrapolate the trajectories of particles that an outside observer sees rising up away from the event horizon. And just as there are two separate interior regions of the maximally extended spacetime, there are also two separate exterior regions, sometimes called two different "universes", with the second universe allowing us to extrapolate some possible particle trajectories in the two interior regions. This means that the interior black hole region can contain a mix of particles that fell in from either universe (and thus an observer who fell in from one universe might be able to see light that fell in from the other one), and likewise particles from the interior white hole region can escape into either universe. All four regions can be seen in a spacetime diagram that uses Kruskal–Szekeres coordinates.

In this spacetime, it is possible to come up with coordinate systems such that if you pick a hypersurface of constant time (a set of points that all have the same time coordinate, such that every point on the surface has a space-like separation, giving what is called a 'space-like surface') and draw an "embedding diagram" depicting the curvature of space at that time, the embedding diagram will look like a tube connecting the two exterior regions, known as an "Einstein–Rosen bridge". Note that the Schwarzschild metric describes an idealized black hole that exists eternally from the perspective of external observers; a more realistic black hole that forms at some particular time from a collapsing star would require a different metric. When the infalling stellar matter is added to a diagram of a black hole's history, it removes the part of the diagram corresponding to the white hole interior region, along with the part of the diagram corresponding to the other universe.

The Einstein–Rosen bridge was discovered by Ludwig Flamm in 1916, a few months after Schwarzschild published his solution, and was rediscovered (although it is hard to imagine that Einstein had not seen Flamm's paper when it came out) by Albert Einstein and his colleague Nathan Rosen, who published their result in 1935. However, in 1962, John A. Wheeler and Robert W. Fuller published a paper showing that this type of wormhole is unstable if it connects two parts of the same universe, and that it will pinch off too quickly for light (or any particle moving slower than light) that falls in from one exterior region to make it to the other exterior region.

According to general relativity, the gravitational collapse of a sufficiently compact mass forms a singular Schwarzschild black hole. In the Einstein–Cartan–Sciama–Kibble theory of gravity, however, it forms a regular Einstein–Rosen bridge. This theory extends general relativity by removing a constraint of the symmetry of the affine connection and regarding its antisymmetric part, the torsion tensor, as a dynamical variable. Torsion naturally accounts for the quantum-mechanical, intrinsic angular momentum (spin) of matter. The minimal coupling between torsion and Dirac spinors generates a repulsive spin–spin interaction that is significant in fermionic matter at extremely high densities. Such an interaction prevents the formation of a gravitational singularity. Instead, the collapsing matter reaches an enormous but finite density and rebounds, forming the other side of the bridge.

Although Schwarzschild wormholes are not traversable in both directions, their existence inspired Kip Thorne to imagine traversable wormholes created by holding the "throat" of a Schwarzschild wormhole open with exotic matter (material that has negative mass/energy).

 

 

Traversable wormholes.

Image of a simulated traversable wormhole that connects the square in front of the physical institutes of University of Tübingen with the sand dunes near Boulogne sur Mer in the north of France. The image is calculated with 4D raytracing in a Morris–Thorne wormhole metric, but the gravitational effects on the wavelength of light have not been simulated.

Lorentzian traversable wormholes would allow travel in both directions from one part of the universe to another part of that same universe very quickly or would allow travel from one universe to another. The possibility of traversable wormholes in general relativity was first demonstrated in a 1973 paper by Homer Ellis and independently in a 1973 paper by K. A. Bronnikov. Ellis thoroughly analyzed the topology and the geodesics of the Ellis drainhole, showing it to be geodesically complete, horizonless, singularity-free, and fully traversable in both directions. The drainhole is a solution manifold of Einstein's field equations for a vacuum space-time, modified by inclusion of a scalar field minimally coupled to the Ricci tensor with antiorthodox polarity (negative instead of positive). (Ellis specifically rejected referring to the scalar field as 'exotic' because of the antiorthodox coupling, finding arguments for doing so unpersuasive.) The solution depends on two parameters: ${\displaystyle m}$, which fixes the strength of its gravitational field, and ${\displaystyle n}$, which determines the curvature of its spatial cross sections. When ${\displaystyle m}$ is set equal to 0, the drainhole's gravitational field vanishes. What is left is the Ellis wormhole, a nongravitating, purely geometric, traversable wormhole. Kip Thorne and his graduate student Mike Morris, unaware of the 1973 papers by Ellis and Bronnikov, manufactured, and in 1988 published, a duplicate of the Ellis wormhole for use as a tool for teaching general relativity. For this reason, the type of traversable wormhole they proposed, held open by a spherical shell of exotic matter, was from 1988 to 2015 exclusively referred to in the literature as a Morris–Thorne wormhole. Later, other types of traversable wormholes were discovered as allowable solutions to the equations of general relativity, including a variety analyzed in a 1989 paper by Matt Visser, in which a path through the wormhole can be made where the traversing path does not pass through a region of exotic matter. However, in the pure Gauss–Bonnet gravity (a modification to general relativity involving extra spatial dimensions which is sometimes studied in the context of brane cosmology) exotic matter is not needed in order for wormholes to exist—they can exist even with no matter. A type held open by negative mass cosmic strings was put forth by Visser in collaboration with Cramer et al., in which it was proposed that such wormholes could have been naturally created in the early universe.

Wormholes connect two points in spacetime, which means that they would in principle allow travel in time, as well as in space. In 1988, Morris, Thorne and Yurtsever worked out explicitly how to convert a wormhole traversing space into one traversing time. However, according to general relativity, it would not be possible to use a wormhole to travel back to a time earlier than when the wormhole was first converted into a time machine by accelerating one of its two mouths.

 

 

Raychaudhuri's theorem and exotic matter

To see why exotic matter is required, consider an incoming light front traveling along geodesics, which then crosses the wormhole and re-expands on the other side. The expansion goes from negative to positive. As the wormhole neck is of finite size, we would not expect caustics to develop, at least within the vicinity of the neck. According to the optical Raychaudhuri's theorem, this requires a violation of the averaged null energy condition. Quantum effects such as the Casimir effect cannot violate the averaged null energy condition in any neighborhood of space with zero curvature, but calculations in semiclassical gravity suggest that quantum effects may be able to violate this condition in curved spacetime. Although it was hoped recently that quantum effects could not violate an achronal version of the averaged null energy condition, violations have nevertheless been found, so it remains an open possibility that quantum effects might be used to support a wormhole.

 

 

Modified general relativity:~

In some theories where general relativity is modified, it is possible to have a wormhole that does not collapse without having to resort to exotic matter. For example, this is possible with R^2 gravity, a form of f(R) gravity.

 

Faster-than-light travel:~

The impossibility of faster-than-light relative speed only applies locally. Wormholes might allow effective superluminal (faster-than-light) travel by ensuring that the speed of light is not exceeded locally at any time. While traveling through a wormhole, subluminal (slower-than-light) speeds are used. If two points are connected by a wormhole whose length is shorter than the distance between them outside the wormhole, the time taken to traverse it could be less than the time it would take a light beam to make the journey if it took a path through the space outside the wormhole. However, a light beam traveling through the wormhole would of course beat the traveler.

 

 

Time travel:~

The theory of general relativity predicts that if traversable wormholes exist, they can also alter the speed of time. They could allow time travel. This would be accomplished by accelerating one end of the wormhole to a high velocity relative to the other, and then sometime later bringing it back; relativistic time dilation would result in the accelerated wormhole mouth aging less than the stationary one as seen by an external observer, similar to what is seen in the twin paradox. However, time connects differently through the wormhole than outside it, so that synchronized clocks at each mouth will remain synchronized to someone traveling through the wormhole itself, no matter how the mouths move around. This means that anything which entered the accelerated wormhole mouth would exit the stationary one at a point in time prior to its entry.

For example, consider two clocks at both mouths both showing the date as 2000. After being taken on a trip at relativistic velocities, the accelerated mouth is brought back to the same region as the stationary mouth with the accelerated mouth's clock reading 2004 while the stationary mouth's clock read 2012. A traveler who entered the accelerated mouth at this moment would exit the stationary mouth when its clock also read 2004, in the same region but now eight years in the past. Such a configuration of wormholes would allow for a particle's world line to form a closed loop in spacetime, known as a closed timelike curve. An object traveling through a wormhole could carry energy or charge from one time to another, but this would not violate conservation of energy or charge in each time, because the energy/charge of the wormhole mouth itself would change to compensate for the object that fell into it or emerged from it.

It is thought that it may not be possible to convert a wormhole into a time machine in this manner; the predictions are made in the context of general relativity, but general relativity does not include quantum effects. Analyses using the semiclassical approach to incorporating quantum effects into general relativity have sometimes indicated that a feedback loop of virtual particles would circulate through the wormhole and pile up on themselves, driving the energy density in the region very high and possibly destroying it before any information could be passed through it, in keeping with the chronology protection conjecture. The debate on this matter is described by Kip S. Thorne in the book Black Holes and Time Warps, and a more technical discussion can be found in The quantum physics of chronology protection by Matt Visser. There is also the Roman ring, which is a configuration of more than one wormhole. This ring seems to allow a closed time loop with stable wormholes when analyzed using semiclassical gravity, although without a full theory of quantum gravity it is uncertain whether the semiclassical approach is reliable in this case.

 

 

Interuniversal travel.

A possible resolution to the paradoxes resulting from wormhole-enabled time travel rests on the many-worlds interpretation of quantum mechanics. In 1991 David Deutsch showed that quantum theory is fully consistent (in the sense that the so-called density matrix can be made free of discontinuities) in spacetimes with closed timelike curves. However, later it was shown that such model of closed timelike curve can have internal inconsistencies as it will lead to strange phenomena like distinguishing non orthogonal quantum states and distinguishing proper and improper mixture. Accordingly, the destructive positive feedback loop of virtual particles circulating through a wormhole time machine, a result indicated by semi-classical calculations, is averted. A particle returning from the future does not return to its universe of origination but to a parallel universe. This suggests that a wormhole time machine with an exceedingly short time jump is a theoretical bridge between contemporaneous parallel universes. Because a wormhole time-machine introduces a type of nonlinearity into quantum theory, this sort of communication between parallel universes is consistent with Joseph Polchinski's discovery of an "Everett phone" in Steven Weinberg's formulation of nonlinear quantum mechanics. Such a possibility is depicted in the science-fiction 2014 movie Interstellar.

 

 

Metrics.

 Theories of wormhole metrics describe the spacetime geometry of a wormhole and serve as theoretical models for time travel. An example of a (traversable) wormhole metric is the following:

${\displaystyle ds^{2}=-c^{2}dt^{2}+dl^{2}+(k^{2}+l^{2})(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}),}$

first presented by Ellis (see Ellis wormhole) as a special case of the Ellis drainhole.
One type of non-traversable wormhole metric is the Schwarzschild solution (see the first diagram):~

${\displaystyle ds^{2}=-c^{2}\left(1-{\frac {2GM}{rc^{2}}}\right)dt^{2}+{\frac {dr^{2}}{1-{\frac {2GM}{rc^{2}}}}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}).}$

The original Einstein-Rosen bridge was described in an article published in July 1935.
For the Schwartzschild spherically symmetric static solution

${\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+(1-{\frac {2m}{r}})dt^{2}}$

(ds = proper time, c = 1)

If one replaces r with u according to ${\displaystyle u^{2}=r-2m}$

${\displaystyle ds^{2}=-4(u^{2}+2m)du^{2}-(u^{2}+2m)^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+{\frac {u^{2}}{u^{2}+2m}}dt^{2}}$

The four-dimensional space is described mathematically by two congruent parts or "sheets", corresponding to u > 0 and u < 0, which are joined by a hyperplane r = 2m or u = 0 in which g vanishes. We call such a connection between the two sheets a "bridge".

For the combined field, gravity and electricity, Einstein and Rosen derived the following Schwarzschild static spherically symmetric solution

${\displaystyle \phi _{1}=\phi _{2}=\phi _{3}=0,\phi _{4}={\frac {\epsilon }{4}},}$

${\displaystyle ds^{2}=-{\frac {1}{(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}})}}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}})dt^{2}}$

( = electrical charge)${\displaystyle \epsilon }$
The field equations without denominators in the case when m = 0 can be written

${\displaystyle \phi _{\mu \nu }=\phi _{\mu ,\nu }-\phi _{\nu ,\mu }}$

${\displaystyle g^{2}\phi _{\mu \nu ;\sigma }g^{\nu \sigma }=0}$

${\displaystyle g^{2}(R_{ik}+\phi _{i\alpha }\phi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\phi _{\alpha \beta }\phi ^{ab})=0}$

In order to eliminate singularities, if one replaces r by u according to the equation:

${\displaystyle u^{2}=r^{2}-{\frac {\epsilon ^{2}}{2}}}$

and with m = 0 one obtains^.

${\displaystyle \phi _{1}=\phi _{2}=\phi _{3}=0,\phi _{4}=\epsilon /(u^{2}+{\frac {\epsilon ^{2}}{2}})^{\frac {1}{2}}}$

${\displaystyle ds^{2}=-du^{2}-(u^{2}+{\frac {\epsilon ^{2}}{2}})(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+({\frac {2u^{2}}{2u^{2}+\epsilon ^{2}}})dt^{2}}$

The solution is free from singularities for all finite points in the space of the two sheets
— A.Einstein,N.Rosen - The Particle Problem in the General Theory of Relativity