Properties of ATOM.

Properties of ATOM.

 

Nuclear properties:~

By definition, any two atoms with an identical number of protons in their nuclei belong to the same chemical element. Atoms with equal numbers of protons but a different number of neutrons are different isotopes of the same element. For example, all hydrogen atoms admit exactly one proton, but isotopes exist with no neutrons (hydrogen-1, by far the most common form, also called protium), one neutron (deuterium), two neutrons (tritium) and more than two neutrons. The known elements form a set of atomic numbers, from the single proton element hydrogen up to the 118-proton element ununoctium. All known isotopes of elements with atomic numbers greater than 82 are radioactive.

About 339 nuclides occur naturally on Earth, of which 254 (about 75%) have not been observed to decay, and are referred to as "stable isotopes". However, only 90 of these nuclides are stable to all decay, even in theory. Another 164 (bringing the total to 254) have not been observed to decay, even though in theory it is energetically possible. These are also formally classified as "stable". An additional 34 radioactive nuclides have half-lives longer than 80 million years, and are long-lived enough to be present from the birth of the solar system. This collection of 288 nuclides are known as primordial nuclides. Finally, an additional 51 short-lived nuclides are known to occur naturally, as daughter products of primordial nuclide decay (such as radium from uranium), or else as products of natural energetic processes on Earth, such as cosmic ray bombardment (for example, carbon-14).

For 80 of the chemical elements, at least one stable isotope exists. As a rule, there is only a handful of stable isotopes for each of these elements, the average being 3.2 stable isotopes per element. Twenty-six elements have only a single stable isotope, while the largest number of stable isotopes observed for any element is ten, for the element tin. Elements 43, 61, and all elements numbered 83 or higher have no stable isotopes.

Stability of isotopes is affected by the ratio of protons to neutrons, and also by the presence of certain "magic numbers" of neutrons or protons that represent closed and filled quantum shells. These quantum shells correspond to a set of energy levels within the shell model of the nucleus; filled shells, such as the filled shell of 50 protons for tin, confers unusual stability on the nuclide. Of the 254 known stable nuclides, only four have both an odd number of protons and odd number of neutrons: hydrogen-2 (deuterium), lithium-6, boron-10 and nitrogen-14. Also, only four naturally occurring, radioactive odd–odd nuclides have a half-life over a billion years: potassium-40, vanadium-50, lanthanum-138 and tantalum-180m. Most odd–odd nuclei are highly unstable with respect to beta decay, because the decay products are even–even, and are therefore more strongly bound, due to nuclear pairing effects.

 

Mass.

The large majority of an atom's mass comes from the protons and neutrons that make it up. The total number of these particles (called "nucleons") in a given atom is called the mass number. It is a positive integer and dimensionless (instead of having dimension of mass), because it expresses a count. An example of use of a mass number is "carbon-12," which has 12 nucleons (six protons and six neutrons).

The actual mass of an atom at rest is often expressed using the unified atomic mass unit (u), also called dalton (Da). This unit is defined as a twelfth of the mass of a free neutral atom of carbon-12, which is approximately 1.66×10⁻²⁷ kg. Hydrogen-1 (the lightest isotope of hydrogen which is also the nuclide with the lowest mass) has an atomic weight of 1.007825 u. The value of this number is called the atomic mass. A given atom has an atomic mass approximately equal (within 1%) to its mass number times the atomic mass unit (for example the mass of a nitrogen-14 is roughly 14 u). However, this number will not be exactly an integer except in the case of carbon-12 (see below). The heaviest stable atom is lead-208, with a mass of 207.9766521 u.

As even the most massive atoms are far too light to work with directly, chemists instead use the unit of moles. One mole of atoms of any element always has the same number of atoms (about 6.022×10²³). This number was chosen so that if an element has an atomic mass of 1 u, a mole of atoms of that element has a mass close to one gram. Because of the definition of the unified atomic mass unit, each carbon-12 atom has an atomic mass of exactly 12 u, and so a mole of carbon-12 atoms weighs exactly 0.012 kg.

 

 

Shape and size:~

Atoms lack a well-defined outer boundary, so their dimensions are usually described in terms of an atomic radius. This is a measure of the distance out to which the electron cloud extends from the nucleus. However, this assumes the atom to exhibit a spherical shape, which is only obeyed for atoms in vacuum or free space. Atomic radii may be derived from the distances between two nuclei when the two atoms are joined in a chemical bond. The radius varies with the location of an atom on the atomic chart, the type of chemical bond, the number of neighboring atoms (coordination number) and a quantum mechanical property known as spin. On the periodic table of the elements, atom size tends to increase when moving down columns, but decrease when moving across rows (left to right). Consequently, the smallest atom is helium with a radius of 32 pm, while one of the largest is caesium at 225 pm.

When subjected to external forces, like electrical fields, the shape of an atom may deviate from spherical symmetry. The deformation depends on the field magnitude and the orbital type of outer shell electrons, as shown by group-theoretical considerations. Aspherical deviations might be elicited for instance in crystals, where large crystal-electrical fields may occur at low-symmetry lattice sites. Significant ellipsoidal deformations have recently been shown to occur for sulfur ions and chalcogen ions in pyrite-type compounds.

Atomic dimensions are thousands of times smaller than the wavelengths of light (400–700 nm) so they cannot be viewed using an optical microscope. However, individual atoms can be observed using a scanning tunneling microscope. To visualize the minuteness of the atom, consider that a typical human hair is about 1 million carbon atoms in width. A single drop of water contains about 2 sextillion (2×10²¹) atoms of oxygen, and twice the number of hydrogen atoms. A single carat diamond with a mass of 2×10⁻⁴ kg contains about 10 sextillion (10²²) atoms of carbon. If an apple were magnified to the size of the Earth, then the atoms in the apple would be approximately the size of the original apple.

Radioactive decay.

This diagram shows the half-life (T_½) of various isotopes with Z protons and N neutrons.

Every element has one or more isotopes that have unstable nuclei that are subject to radioactive decay, causing the nucleus to emit particles or electromagnetic radiation. Radioactivity can occur when the radius of a nucleus is large compared with the radius of the strong force, which only acts over distances on the order of 1 fm.

• Alpha decay: this process is caused when the nucleus emits an alpha particle, which is a helium nucleus consisting of two protons and two neutrons. The result of the emission is a new element with a lower atomic number.
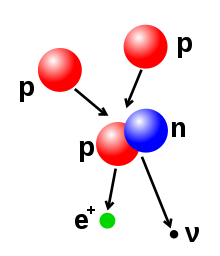
• Beta decay (and electron capture): these processes are regulated by the weak force, and result from a transformation of a neutron into a proton, or a proton into a neutron. The neutron to proton transition is accompanied by the emission of an electron and an antineutrino, while proton to neutron transition (except in electron capture) causes the emission of a positron and a neutrino. The electron or positron emissions are called beta particles. Beta decay either increases or decreases the atomic number of the nucleus by one. Electron capture is more common than positron emission, because it requires less energy. In this type of decay, an electron is absorbed by the nucleus, rather than a positron emitted from the nucleus. A neutrino is still emitted in this process, and a proton changes to a neutron.
• Gamma decay: this process results from a change in the energy level of the nucleus to a lower state, resulting in the emission of electromagnetic radiation. The excited state of a nucleus which results in gamma emission usually occurs following the emission of an alpha or a beta particle. Thus, gamma decay usually follows alpha or beta decay.

Other more rare types of radioactive decay include ejection of neutrons or protons or clusters of nucleons from a nucleus, or more than one beta particle. An analog of gamma emission which allows excited nuclei to lose energy in a different way, is internal conversion— a process that produces high-speed electrons that are not beta rays, followed by production of high-energy photons that are not gamma rays. A few large nuclei explode into two or more charged fragments of varying masses plus several neutrons, in a decay called spontaneous nuclear fission.

Each radioactive isotope has a characteristic decay time period—the half-life—that is determined by the amount of time needed for half of a sample to decay. This is an exponential decay process that steadily decreases the proportion of the remaining isotope by 50% every half-life. Hence after two half-lives have passed only 25% of the isotope is present, and so forth.

 

 

Magnetic moment.

Elementary particles possess an intrinsic quantum mechanical property known as spin. This is analogous to the angular momentum of an object that is spinning around its center of mass, although strictly speaking these particles are believed to be point-like and cannot be said to be rotating. Spin is measured in units of the reduced Planck constant (ħ), with electrons, protons and neutrons all having spin ½ ħ, or "spin-½". In an atom, electrons in motion around the nucleus possess orbital angular momentum in addition to their spin, while the nucleus itself possesses angular momentum due to its nuclear spin.

The magnetic field produced by an atom—its magnetic moment—is determined by these various forms of angular momentum, just as a rotating charged object classically produces a magnetic field. However, the most dominant contribution comes from electron spin. Due to the nature of electrons to obey the Pauli exclusion principle, in which no two electrons may be found in the same quantum state, bound electrons pair up with each other, with one member of each pair in a spin up state and the other in the opposite, spin down state. Thus these spins cancel each other out, reducing the total magnetic dipole moment to zero in some atoms with even number of electrons.
 
In ferromagnetic elements such as iron, cobalt and nickel, an odd number of electrons leads to an unpaired electron and a net overall magnetic moment. The orbitals of neighboring atoms overlap and a lower energy state is achieved when the spins of unpaired electrons are aligned with each other, a spontaneous process known as an exchange interaction. When the magnetic moments of ferromagnetic atoms are lined up, the material can produce a measurable macroscopic field. Paramagnetic materials have atoms with magnetic moments that line up in random directions when no magnetic field is present, but the magnetic moments of the individual atoms line up in the presence of a field.

The nucleus of an atom will have no spin when it has even numbers of both neutrons and protons, but for other cases of odd numbers, the nucleus may have a spin. Normally nuclei with spin are aligned in random directions because of thermal equilibrium. However, for certain elements (such as xenon-129) it is possible to polarize a significant proportion of the nuclear spin states so that they are aligned in the same direction—a condition called hyperpolarization. This has important applications in magnetic resonance imaging.

 

 

Energy levels.

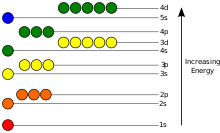These electron's energy levels (not to scale) are sufficient for ground states of atoms up to cadmium (5s² 4d¹⁰) inclusively. Do not forget that even the top of the diagram is lower than an unbound electron state.

The potential energy of an electron in an atom is negative, its dependence of its position reaches the minimum (the most absolute value) inside the nucleus, and vanishes when the distance from the nucleus goes to infinity, roughly in an inverse proportion to the distance. In the quantum-mechanical model, a bound electron can only occupy a set of states centered on the nucleus, and each state corresponds to a specific energy level; see time-independent Schrödinger equation for theoretical explanation. An energy level can be measured by the amount of energy needed to unbind the electron from the atom, and is usually given in units of electronvolts (eV). The lowest energy state of a bound electron is called the ground state, i.e. stationary state, while an electron transition to a higher level results in an excited state. The electron's energy raises when n increases because the (average) distance to the nucleus increases. Dependence of the energy on ℓ is caused not by electrostatic potential of the nucleus, but by interaction between electrons.

For an electron to transition between two different states, e.g. grounded state to first excited level (ionization), it must absorb or emit a photon at an energy matching the difference in the potential energy of those levels, according to Niels Bohr model, what can be precisely calculated by the Schrödinger equation. Electrons jump between orbitals in a particle-like fashion. For example, if a single photon strikes the electrons, only a single electron changes states in response to the photon; see Electron properties.

The energy of an emitted photon is proportional to its frequency, so these specific energy levels appear as distinct bands in the electromagnetic spectrum. Each element has a characteristic spectrum that can depend on the nuclear charge, subshells filled by electrons, the electromagnetic interactions between the electrons and other factors.

An example of absorption lines in a spectrum

When a continuous spectrum of energy is passed through a gas or plasma, some of the photons are absorbed by atoms, causing electrons to change their energy level. Those excited electrons that remain bound to their atom spontaneously emit this energy as a photon, traveling in a random direction, and so drop back to lower energy levels. Thus the atoms behave like a filter that forms a series of dark absorption bands in the energy output. (An observer viewing the atoms from a view that does not include the continuous spectrum in the background, instead sees a series of emission lines from the photons emitted by the atoms.) Spectroscopic measurements of the strength and width of atomic spectral lines allow the composition and physical properties of a substance to be determined.

Close examination of the spectral lines reveals that some display a fine structure splitting. This occurs because of spin–orbit coupling, which is an interaction between the spin and motion of the outermost electron. When an atom is in an external magnetic field, spectral lines become split into three or more components; a phenomenon called the Zeeman effect. This is caused by the interaction of the magnetic field with the magnetic moment of the atom and its electrons. Some atoms can have multiple electron configurations with the same energy level, which thus appear as a single spectral line. The interaction of the magnetic field with the atom shifts these electron configurations to slightly different energy levels, resulting in multiple spectral lines. The presence of an external electric field can cause a comparable splitting and shifting of spectral lines by modifying the electron energy levels, a phenomenon called the Stark effect.

If a bound electron is in an excited state, an interacting photon with the proper energy can cause stimulated emission of a photon with a matching energy level. For this to occur, the electron must drop to a lower energy state that has an energy difference matching the energy of the interacting photon. The emitted photon and the interacting photon then move off in parallel and with matching phases. That is, the wave patterns of the two photons are synchronized. This physical property is used to make lasers, which can emit a coherent beam of light energy in a narrow frequency band.

 

 

Valence and bonding behavior.

Valency is the combining power of an element. It is equal to number of hydrogen atoms that atom can combine or displace in forming compounds. The outermost electron shell of an atom in its uncombined state is known as the valence shell, and the electrons in that shell are called valence electrons. The number of valence electrons determines the bonding behavior with other atoms. Atoms tend to chemically react with each other in a manner that fills (or empties) their outer valence shells. For example, a transfer of a single electron between atoms is a useful approximation for bonds that form between atoms with one-electron more than a filled shell, and others that are one-electron short of a full shell, such as occurs in the compound sodium chloride and other chemical ionic salts. However, many elements display multiple valences, or tendencies to share differing numbers of electrons in different compounds. Thus, chemical bonding between these elements takes many forms of electron-sharing that are more than simple electron transfers. Examples include the element carbon and the organic compounds.

The chemical elements are often displayed in a periodic table that is laid out to display recurring chemical properties, and elements with the same number of valence electrons form a group that is aligned in the same column of the table. (The horizontal rows correspond to the filling of a quantum shell of electrons.) The elements at the far right of the table have their outer shell completely filled with electrons, which results in chemically inert elements known as the noble gases.

 

 

States.

Snapshots illustrating the formation of a Bose–Einstein condensate

Quantities of atoms are found in different states of matter that depend on the physical conditions, such as temperature and pressure. By varying the conditions, materials can transition between solids, liquids, gases and plasmas. Within a state, a material can also exist in different allotropes. An example of this is solid carbon, which can exist as graphite or diamond. Gaseous allotropes exist as well, such as dioxygen and ozone.

At temperatures close to absolute zero, atoms can form a Bose–Einstein condensate, at which point quantum mechanical effects, which are normally only observed at the atomic scale, become apparent on a macroscopic scale. This super-cooled collection of atoms then behaves as a single super atom, which may allow fundamental checks of quantum mechanical behavior.

Atom.

An atom is the smallest constituent unit of ordinary matter that has the properties of a chemical element. Every solid, liquid, gas, and plasma is composed of neutral or ionized atoms. Atoms are very small; typical sizes are around 100 pm (a ten-billionth of a meter, in the short scale). However, atoms do not have well-defined boundaries, and there are different ways to define their size that give different but close values.

Atoms are small enough that attempting to predict their behavior using classical physics - as if they were billiard balls, for example - gives noticeably incorrect predictions due to quantum effects. Through the development of physics, atomic models have incorporated quantum principles to better explain and predict the behavior.

Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and typically a similar number of neutrons. Protons and neutrons are called nucleons. More than 99.94% of an atom's mass is in the nucleus. The protons have a positive electric charge, the electrons have a negative electric charge, and the neutrons have no electric charge. If the number of protons and electrons are equal, that atom is electrically neutral. If an atom has more or fewer electrons than protons, then it has an overall negative or positive charge, respectively, and it is called an ion.

The electrons of an atom are attracted to the protons in an atomic nucleus by this electromagnetic force. The protons and neutrons in the nucleus are attracted to each other by a different force, the nuclear force, which is usually stronger than the electromagnetic force repelling the positively charged protons from one another. Under certain circumstances the repelling electromagnetic force becomes stronger than the nuclear force, and nucleons can be ejected from the nucleus, leaving behind a different element: nuclear decay resulting in nuclear transmutation.

The number of protons in the nucleus defines to what chemical element the atom belongs: for example, all copper atoms contain 29 protons. The number of neutrons defines the isotope of the element. The number of electrons influences the magnetic properties of an atom. Atoms can attach to one or more other atoms by chemical bonds to form chemical compounds such as molecules. The ability of atoms to associate and dissociate is responsible for most of the physical changes observed in nature, and is the subject of the discipline of chemistry.

 

History of atomic theory.

 

Atoms in philosophy:~

The idea that matter is made up of discrete units is a very old idea, appearing in many ancient cultures such as Greece and India. The word "atom" was coined by ancient Greek philosophers. However, these ideas were founded in philosophical and theological reasoning rather than evidence and experimentation. As a result, their views on what atoms look like and how they behave were incorrect. They also could not convince everybody, so atomism was but one of a number of competing theories on the nature of matter. It was not until the 19th century that the idea was embraced and refined by scientists, when the blossoming science of chemistry produced discoveries that only the concept of atoms could explain.

 

 

First evidence-based theory:~

Various atoms and molecules as depicted in John Dalton's A New System of Chemical Philosophy (1808).

In the early 1800s, John Dalton used the concept of atoms to explain why elements always react in ratios of small whole numbers (the law of multiple proportions). For instance, there are two types of tin oxide: one is 88.1% tin and 11.9% oxygen and the other is 78.7% tin and 21.3% oxygen (tin(II) oxide and tin dioxide respectively). This means that 100g of tin will combine either with 13.5g or 27g of oxygen. 13.5 and 27 form a ratio of 1:2, a ratio of small whole numbers. This common pattern in chemistry suggested to Dalton that elements react in whole number multiples of discrete units—in other words, atoms. In the case of tin oxides, one tin atom will combine with either one or two oxygen atoms.

Dalton also believed atomic theory could explain why water absorbs different gases in different proportions. For example, he found that water absorbs carbon dioxide far better than it absorbs nitrogen. Dalton hypothesized this was due to the differences between the masses and configurations of the gases' respective particles, and carbon dioxide molecules (CO₂) are heavier and larger than nitrogen molecules (N₂).

 

 

Brownian motion:~

In 1827, botanist Robert Brown used a microscope to look at dust grains floating in water and discovered that they moved about erratically, a phenomenon that became known as "Brownian motion". This was thought to be caused by water molecules knocking the grains about. In 1905 Albert Einstein proved the reality of these molecules and their motions by producing the first Statistical physics analysis of Brownian motion. French physicist Jean Perrin used Einstein's work to experimentally determine the mass and dimensions of atoms, thereby conclusively verifying Dalton's atomic theory.

 

Discovery of the electron.

 

The Geiger–Marsden experiment
Top: Expected results: alpha particles passing through the plum pudding model of the atom with negligible deflection.
Bottom: Observed results: a small portion of the particles were deflected by the concentrated positive charge of the nucleus.

The physicist J. J. Thomson measured the mass of cathode rays, showing they were made of particles, but were around 1800 times lighter than the lightest atom, hydrogen. Therefore, they were not atoms, but a new particle, the first subatomic particle to be discovered, which he originally called "corpuscle" but was later named electron, after particles postulated by George Johnstone Stoney in 1874. He also showed they were identical to particles given off by photoelectric and radioactive materials. It was quickly recognized that they are the particles that carry electric currents in metal wires, and carry the negative electric charge within atoms. Thomson was given the 1906 Nobel Prize in Physics for this work. Thus he overturned the belief that atoms are the indivisible, ultimate particles of matter. Thomson also incorrectly postulated that the low mass, negatively charged electrons were distributed throughout the atom in a uniform sea of positive charge. This became known as the plum pudding model.

 

 

Discovery of the nucleus.

 

In 1909, Hans Geiger and Ernest Marsden, under the direction of Ernest Rutherford, bombarded a metal foil with alpha particles to observe how they scattered. They expected all the alpha particles to pass straight through with little deflection, because Thomson's model said that the charges in the atom are so diffuse that their electric fields could not affect the alpha particles much. However, Geiger and Marsden spotted alpha particles being deflected by angles greater than 90°, which was supposed to be impossible according to Thomson's model. To explain this, Rutherford proposed that the positive charge of the atom is concentrated in a tiny nucleus at the center of the atom.

 

Discovery of isotopes.

While experimenting with the products of radioactive decay, in 1913 radiochemist Frederick Soddy discovered that there appeared to be more than one type of atom at each position on the periodic table. The term isotope was coined by Margaret Todd as a suitable name for different atoms that belong to the same element. J.J. Thomson created a technique for separating atom types through his work on ionized gases, which subsequently led to the discovery of stable isotopes.

 

 

Bohr model.

 

The Bohr model of the atom, with an electron making instantaneous "quantum leaps" from one orbit to another. This model is obsolete.

In 1913 the physicist Niels Bohr proposed a model in which the electrons of an atom were assumed to orbit the nucleus but could only do so in a finite set of orbits, and could jump between these orbits only in discrete changes of energy corresponding to absorption or radiation of a photon. This quantization was used to explain why the electrons orbits are stable (given that normally, charges in acceleration, including circular motion, lose kinetic energy which is emitted as electromagnetic radiation, see synchrotron radiation) and why elements absorb and emit electromagnetic radiation in discrete spectra.

Later in the same year Henry Moseley provided additional experimental evidence in favor of Niels Bohr's theory. These results refined Ernest Rutherford's and Antonius Van den Broek's model, which proposed that the atom contains in its nucleus a number of positive nuclear charges that is equal to its (atomic) number in the periodic table. Until these experiments, atomic number was not known to be a physical and experimental quantity. That it is equal to the atomic nuclear charge remains the accepted atomic model today.

 

 

Chemical bonding explained:~

Chemical bonds between atoms were now explained, by Gilbert Newton Lewis in 1916, as the interactions between their constituent electrons. As the chemical properties of the elements were known to largely repeat themselves according to the periodic law, in 1919 the American chemist Irving Langmuir suggested that this could be explained if the electrons in an atom were connected or clustered in some manner. Groups of electrons were thought to occupy a set of electron shells about the nucleus.

 

 

Further developments in quantum physics.

The Stern–Gerlach experiment of 1922 provided further evidence of the quantum nature of the atom. When a beam of silver atoms was passed through a specially shaped magnetic field, the beam was split based on the direction of an atom's angular momentum, or spin. As this direction is random, the beam could be expected to spread into a line. Instead, the beam was split into two parts, depending on whether the atomic spin was oriented up or down.

In 1924, Louis de Broglie proposed that all particles behave to an extent like waves. In 1926, Erwin Schrödinger used this idea to develop a mathematical model of the atom that described the electrons as three-dimensional waveforms rather than point particles. A consequence of using waveforms to describe particles is that it is mathematically impossible to obtain precise values for both the position and momentum of a particle at a given point in time; this became known as the uncertainty principle, formulated by Werner Heisenberg in 1926. In this concept, for a given accuracy in measuring a position one could only obtain a range of probable values for momentum, and vice versa. This model was able to explain observations of atomic behavior that previous models could not, such as certain structural and spectral patterns of atoms larger than hydrogen. Thus, the planetary model of the atom was discarded in favor of one that described atomic orbital zones around the nucleus where a given electron is most likely to be observed.

 

 

Discovery of the neutron.

The development of the mass spectrometer allowed the mass of atoms to be measured with increased accuracy. The device uses a magnet to bend the trajectory of a beam of ions, and the amount of deflection is determined by the ratio of an atom's mass to its charge. The chemist Francis William Aston used this instrument to show that isotopes had different masses. The atomic mass of these isotopes varied by integer amounts, called the whole number rule. The explanation for these different isotopes awaited the discovery of the neutron, an uncharged particle with a mass similar to the proton, by the physicist James Chadwick in 1932. Isotopes were then explained as elements with the same number of protons, but different numbers of neutrons within the nucleus.

 

 

Fission, high-energy physics and condensed matter.

In 1938, the German chemist Otto Hahn, a student of Rutherford, directed neutrons onto uranium atoms expecting to get transuranium elements. Instead, his chemical experiments showed barium as a product. A year later, Lise Meitner and her nephew Otto Frisch verified that Hahn's result were the first experimental nuclear fission. In 1944, Hahn received the Nobel prize in chemistry. Despite Hahn's efforts, the contributions of Meitner and Frisch were not recognized.

In the 1950s, the development of improved particle accelerators and particle detectors allowed scientists to study the impacts of atoms moving at high energies. Neutrons and protons were found to be hadrons, or composites of smaller particles called quarks. The standard model of particle physics was developed that so far has successfully explained the properties of the nucleus in terms of these sub-atomic particles and the forces that govern their interactions.

 

 

Structure.

Subatomic particles:~

Though the word atom originally denoted a particle that cannot be cut into smaller particles, in modern scientific usage the atom is composed of various subatomic particles. The constituent particles of an atom are the electron, the proton and the neutron; all three are fermions. However, the hydrogen-1 atom has no neutrons and the hydron ion has no electrons.

The electron is by far the least massive of these particles at 9.11×10⁻³¹ kg, with a negative electrical charge and a size that is too small to be measured using available techniques. It is the lightest particle with a positive rest mass measured. Under ordinary conditions, electrons are bound to the positively charged nucleus by the attraction created from opposite electric charges. If an atom has more or fewer electrons than its atomic number, then it becomes respectively negatively or positively charged as a whole; a charged atom is called an ion. Electrons have been known since the late 19th century, mostly thanks to J.J. Thomson; see history of subatomic physics for details.

Protons have a positive charge and a mass 1,836 times that of the electron, at 1.6726×10⁻²⁷ kg. The number of protons in an atom is called its atomic number. Ernest Rutherford (1919) observed that nitrogen under alpha-particle bombardment ejects what appeared to be hydrogen nuclei. By 1920 he had accepted that the hydrogen nucleus is a distinct particle within the atom and named it proton.

Neutrons have no electrical charge and have a free mass of 1,839 times the mass of the electron, or 1.6929×10⁻²⁷ kg, the heaviest of the three constituent particles, but it can be reduced by the nuclear binding energy. Neutrons and protons (collectively known as nucleons) have comparable dimensions—on the order of 2.5×10⁻¹⁵ m—although the 'surface' of these particles is not sharply defined. The neutron was discovered in 1932 by the English physicist James Chadwick.

In the Standard Model of physics, electrons are truly elementary particles with no internal structure. However, both protons and neutrons are composite particles composed of elementary particles called quarks. There are two types of quarks in atoms, each having a fractional electric charge. Protons are composed of two up quarks (each with charge +2/3) and one down quark (with a charge of −1/3). Neutrons consist of one up quark and two down quarks. This distinction accounts for the difference in mass and charge between the two particles.

The quarks are held together by the strong interaction (or strong force), which is mediated by gluons. The protons and neutrons, in turn, are held to each other in the nucleus by the nuclear force, which is a residuum of the strong force that has somewhat different range-properties (see the article on the nuclear force for more). The gluon is a member of the family of gauge bosons, which are elementary particles that mediate physical forces.

 

 

Nucleus.

The binding energy needed for a nucleon to escape the nucleus, for various isotopes

All the bound protons and neutrons in an atom make up a tiny atomic nucleus, and are collectively called nucleons. The radius of a nucleus is approximately equal to 1.07 ³√A fm, where A is the total number of nucleons. This is much smaller than the radius of the atom, which is on the order of 10⁵ fm. The nucleons are bound together by a short-ranged attractive potential called the residual strong force. At distances smaller than 2.5 fm this force is much more powerful than the electrostatic force that causes positively charged protons to repel each other.
 
Atoms of the same element have the same number of protons, called the atomic number. Within a single element, the number of neutrons may vary, determining the isotope of that element. The total number of protons and neutrons determine the nuclide. The number of neutrons relative to the protons determines the stability of the nucleus, with certain isotopes undergoing radioactive decay.

The proton, the electron, and the neutron are classified as fermions. Fermions obey the Pauli exclusion principle which prohibits identical fermions, such as multiple protons, from occupying the same quantum state at the same time. Thus, every proton in the nucleus must occupy a quantum state different from all other protons, and the same applies to all neutrons of the nucleus and to all electrons of the electron cloud. However, a proton and a neutron are allowed to occupy the same quantum state.

For atoms with low atomic numbers, a nucleus that has more neutrons than protons tends to drop to a lower energy state through radioactive decay so that the neutron–proton ratio is closer to one. However, as the atomic number increases, a higher proportion of neutrons is required to offset the mutual repulsion of the protons. Thus, there are no stable nuclei with equal proton and neutron numbers above atomic number Z = 20 (calcium) and as Z increases, the neutron–proton ratio of stable isotopes increases. The stable isotope with the highest proton–neutron ratio is lead-208 (about 1.5).

Illustration of a nuclear fusion process that forms a deuterium nucleus, consisting of a proton and a neutron, from two protons. A positron (e⁺)—an antimatter electron—is emitted along with an electron neutrino.

The number of protons and neutrons in the atomic nucleus can be modified, although this can require very high energies because of the strong force. Nuclear fusion occurs when multiple atomic particles join to form a heavier nucleus, such as through the energetic collision of two nuclei. For example, at the core of the Sun protons require energies of 3–10 keV to overcome their mutual repulsion—the coulomb barrier—and fuse together into a single nucleus. Nuclear fission is the opposite process, causing a nucleus to split into two smaller nuclei—usually through radioactive decay. The nucleus can also be modified through bombardment by high energy subatomic particles or photons. If this modifies the number of protons in a nucleus, the atom changes to a different chemical element.

If the mass of the nucleus following a fusion reaction is less than the sum of the masses of the separate particles, then the difference between these two values can be emitted as a type of usable energy (such as a gamma ray, or the kinetic energy of a beta particle), as described by Albert Einstein's mass–energy equivalence formula, E = mc², where m is the mass loss and c is the speed of light. This deficit is part of the binding energy of the new nucleus, and it is the non-recoverable loss of the energy that causes the fused particles to remain together in a state that requires this energy to separate.

The fusion of two nuclei that create larger nuclei with lower atomic numbers than iron and nickel—a total nucleon number of about 60—is usually an exothermic process that releases more energy than is required to bring them together. It is this energy-releasing process that makes nuclear fusion in stars a self-sustaining reaction. For heavier nuclei, the binding energy per nucleon in the nucleus begins to decrease. That means fusion processes producing nuclei that have atomic numbers higher than about 26, and atomic masses higher than about 60, is an endothermic process. These more massive nuclei can not undergo an energy-producing fusion reaction that can sustain the hydrostatic equilibrium of a star.

 

 

Electron cloud.

 

A potential well, showing, according to classical mechanics, the minimum energy V(x) needed to reach each position x. Classically, a particle with energy E is constrained to a range of positions between x₁ and x₂.

The electrons in an atom are attracted to the protons in the nucleus by the electromagnetic force. This force binds the electrons inside an electrostatic potential well surrounding the smaller nucleus, which means that an external source of energy is needed for the electron to escape. The closer an electron is to the nucleus, the greater the attractive force. Hence electrons bound near the center of the potential well require more energy to escape than those at greater separations.

Electrons, like other particles, have properties of both a particle and a wave. The electron cloud is a region inside the potential well where each electron forms a type of three-dimensional standing wave—a wave form that does not move relative to the nucleus. This behavior is defined by an atomic orbital, a mathematical function that characterises the probability that an electron appears to be at a particular location when its position is measured. Only a discrete (or quantized) set of these orbitals exist around the nucleus, as other possible wave patterns rapidly decay into a more stable form. Orbitals can have one or more ring or node structures, and differ from each other in size, shape and orientation.

Wave functions of the first five atomic orbitals. The three 2p orbitals each display a single angular node that has an orientation and a minimum at the center.

Each atomic orbital corresponds to a particular energy level of the electron. The electron can change its state to a higher energy level by absorbing a photon with sufficient energy to boost it into the new quantum state. Likewise, through spontaneous emission, an electron in a higher energy state can drop to a lower energy state while radiating the excess energy as a photon. These characteristic energy values, defined by the differences in the energies of the quantum states, are responsible for atomic spectral lines.

The amount of energy needed to remove or add an electron—the electron binding energy—is far less than the binding energy of nucleons. For example, it requires only 13.6 eV to strip a ground-state electron from a hydrogen atom, compared to 2.23 million eV for splitting a deuterium nucleus. Atoms are electrically neutral if they have an equal number of protons and electrons. Atoms that have either a deficit or a surplus of electrons are called ions. Electrons that are farthest from the nucleus may be transferred to other nearby atoms or shared between atoms. By this mechanism, atoms are able to bond into molecules and other types of chemical compounds like ionic and covalent network crystals.