Event horizon

Event horizon.

Far away from the black hole, a particle can move in any direction, as illustrated by the set of arrows. It is only restricted by the speed of light.

The defining feature of a black hole is the appearance of an event horizon—a boundary in spacetime through which matter and light can only pass inward towards the mass of the black hole. Nothing, not even light, can escape from inside the event horizon. The event horizon is referred to as such because if an event occurs within the boundary, information from that event cannot reach an outside observer, making it impossible to determine if such an event occurred.

As predicted by general relativity, the presence of a mass deforms spacetime in such a way that the paths taken by particles bend towards the mass. At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.

Closer to the black hole, spacetime starts to deform. There are more paths going towards the black hole than paths moving away

To a distant observer, clocks near a black hole appear to tick more slowly than those further away from the black hole. Due to this effect, known as gravitational time dilation, an object falling into a black hole appears to slow as it approaches the event horizon, taking an infinite time to reach it. At the same time, all processes on this object slow down, from the view point of a fixed outside observer, causing any light emitted by the object to appear redder and dimmer, an effect known as gravitational redshift. Eventually, the falling object becomes so dim that it can no longer be seen.

On the other hand, indestructible observers falling into a black hole do not notice any of these effects as they cross the event horizon. According to their own clocks, which appear to them to tick normally, they cross the event horizon after a finite time without noting any singular behaviour; it is impossible to determine the location of the event horizon from local observations.

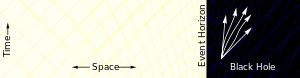Inside of the event horizon, all paths bring the particle closer to the center of the black hole. It is no longer possible for the particle to escape.

The shape of the event horizon of a black hole is always approximately spherical. For non-rotating (static) black holes the geometry of the event horizon is precisely spherical, while for rotating black holes the sphere is oblate.

 

Singularity:~

At the center of a black hole, as described by general relativity, lies a gravitational singularity, a region where the spacetime curvature becomes infinite. For a non-rotating black hole, this region takes the shape of a single point and for a rotating black hole, it is smeared out to form a ring singularity that lies in the plane of rotation. In both cases, the singular region has zero volume. It can also be shown that the singular region contains all the mass of the black hole solution. The singular region can thus be thought of as having infinite density.

Observers falling into a Schwarzschild black hole (i.e., non-rotating and not charged) cannot avoid being carried into the singularity, once they cross the event horizon. They can prolong the experience by accelerating away to slow their descent, but only up to a limit; after attaining a certain ideal velocity, it is best to free fall the rest of the way. When they reach the singularity, they are crushed to infinite density and their mass is added to the total of the black hole. Before that happens, they will have been torn apart by the growing tidal forces in a process sometimes referred to as spaghettification or the "noodle effect".

In the case of a charged (Reissner–Nordström) or rotating (Kerr) black hole, it is possible to avoid the singularity. Extending these solutions as far as possible reveals the hypothetical possibility of exiting the black hole into a different spacetime with the black hole acting as a wormhole. The possibility of traveling to another universe is, however, only theoretical since any perturbation would destroy this possibility. It also appears to be possible to follow closed timelike curves (returning to one's own past) around the Kerr singularity, which lead to problems with causality like the grandfather paradox. It is expected that none of these peculiar effects would survive in a proper quantum treatment of rotating and charged black holes.

The appearance of singularities in general relativity is commonly perceived as signaling the breakdown of the theory. This breakdown, however, is expected; it occurs in a situation where quantum effects should describe these actions, due to the extremely high density and therefore particle interactions. To date, it has not been possible to combine quantum and gravitational effects into a single theory, although there exist attempts to formulate such a theory of quantum gravity. It is generally expected that such a theory will not feature any singularities.

 

Photon sphere:~

The photon sphere is a spherical boundary of zero thickness in which photons that move on tangents to that sphere would be trapped in a circular orbit about the black hole. For non-rotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius. Their orbits would be dynamically unstable, hence any small perturbation, such as a particle of infalling matter, would cause an instability that would grow over time, either setting the photon on an outward trajectory causing it to escape the black hole, or on an inward spiral where it would eventually cross the event horizon.

While light can still escape from the photon sphere, any light that crosses the photon sphere on an inbound trajectory will be captured by the black hole. Hence any light that reaches an outside observer from the photon sphere must have been emitted by objects between the photon sphere and the event horizon.

Other compact objects, such as neutron stars, can also have photon spheres. This follows from the fact that the gravitational field external to a spherically-symmetric object is governed by the Schwarzschild metric, which depends only on the object's mass rather than the radius of the object, hence any object whose radius shrinks to smaller than 1.5 times the Schwarzschild radius will have photon sphere.

 

Ergosphere.

Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere. This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly "drag" along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole, this effect is so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.

The ergosphere is an oblate spheroid region outside of the event horizon, where objects cannot remain stationary.

The ergosphere of a black hole is a volume whose inner boundary is the black hole's event horizon and an outer boundary of an oblate spheroid, which coincides with the event horizon at the poles but noticeably wider around the equator. The outer boundary is sometimes called the ergosurface.
Objects and radiation can escape normally from the ergosphere. Through the Penrose process, objects can emerge from the ergosphere with more energy than they entered. This energy is taken from the rotational energy of the black hole causing the latter to slow.

 

Innermost stable circular orbit (ISCO):~

In Newtonian gravity, test particles can stably orbit at arbitrary distances from a central object. In general relativity, however, there exists an innermost stable circular orbit (often called the ISCO), inside of which, any infinitesimal perturbations to a circular orbit will lead to inspiral into the black hole. The location of the ISCO depends on the spin of the black hole, in the case of a Schwarzschild black hole (spin zero) is:

${\displaystyle r_{isco}=3\,r_{s}={\frac {6\,GM}{c^{2}}},}$

and decreases with increasing spin.

 

Formation and evolution:~

Considering the exotic nature of black holes, it may be natural to question if such bizarre objects could exist in nature or to suggest that they are merely pathological solutions to Einstein's equations. Einstein himself wrongly thought that black holes would not form, because he held that the angular momentum of collapsing particles would stabilize their motion at some radius. This led the general relativity community to dismiss all results to the contrary for many years. However, a minority of relativists continued to contend that black holes were physical objects, and by the end of the 1960s, they had persuaded the majority of researchers in the field that there is no obstacle to the formation of an event horizon.

Once an event horizon forms, Penrose proved, general relativity without quantum mechanics requires that a singularity will form within. Shortly afterwards, Hawking showed that many cosmological solutions that describe the Big Bang have singularities without scalar fields or other exotic matter (see "Penrose–Hawking singularity theorems"). The Kerr solution, the no-hair theorem, and the laws of black hole thermodynamics showed that the physical properties of black holes were simple and comprehensible, making them respectable subjects for research. The primary formation process for black holes is expected to be the gravitational collapse of heavy objects such as stars, but there are also more exotic processes that can lead to the production of black holes.

 

Gravitational collapse:~

Gravitational collapse occurs when an object's internal pressure is insufficient to resist the object's own gravity. For stars this usually occurs either because a star has too little "fuel" left to maintain its temperature through stellar nucleosynthesis, or because a star that would have been stable receives extra matter in a way that does not raise its core temperature. In either case the star's temperature is no longer high enough to prevent it from collapsing under its own weight. The collapse may be stopped by the degeneracy pressure of the star's constituents, allowing the condensation of matter into an exotic denser state. The result is one of the various types of compact star. The type of compact star formed depends on the mass of the remnant of the original star left after the outer layers have been blown away. Such explosions and pulsations lead to planetary nebula. This mass can be substantially less than the original star. Remnants exceeding 5 M_☉ are produced by stars that were over 20 M_☉ before the collapse.

If the mass of the remnant exceeds about 3–4 M_☉ (the Tolman–Oppenheimer–Volkoff limit), either because the original star was very heavy or because the remnant collected additional mass through accretion of matter, even the degeneracy pressure of neutrons is insufficient to stop the collapse. No known mechanism (except possibly quark degeneracy pressure, see quark star) is powerful enough to stop the implosion and the object will inevitably collapse to form a black hole.

Artist’s impression of supermassive black hole seed.

The gravitational collapse of heavy stars is assumed to be responsible for the formation of stellar mass black holes. Star formation in the early universe may have resulted in very massive stars, which upon their collapse would have produced black holes of up to 10³ M_☉. These black holes could be the seeds of the supermassive black holes found in the centers of most galaxies. It has further been suggested that supermassive black holes with typical masses of ~10⁵ M_☉ could have formed from the direct collapse of gas clouds in the young universe. Some candidates for such objects have been found in observations of the young universe.

While most of the energy released during gravitational collapse is emitted very quickly, an outside observer does not actually see the end of this process. Even though the collapse takes a finite amount of time from the reference frame of infalling matter, a distant observer would see the infalling material slow and halt just above the event horizon, due to gravitational time dilation. Light from the collapsing material takes longer and longer to reach the observer, with the light emitted just before the event horizon forms delayed an infinite amount of time. Thus the external observer never sees the formation of the event horizon; instead, the collapsing material seems to become dimmer and increasingly red-shifted, eventually fading away.

 

Primordial black holes in the Big Bang:~

Gravitational collapse requires great density. In the current epoch of the universe these high densities are only found in stars, but in the early universe shortly after the big bang densities were much greater, possibly allowing for the creation of black holes. The high density alone is not enough to allow the formation of black holes since a uniform mass distribution will not allow the mass to bunch up. In order for primordial black holes to form in such a dense medium, there must be initial density perturbations that can then grow under their own gravity. Different models for the early universe vary widely in their predictions of the size of these perturbations. Various models predict the creation of black holes, ranging from a Planck mass to hundreds of thousands of solar masses. Primordial black holes could thus account for the creation of any type of black hole.

 

High-energy collisions.

A simulated event in the CMS detector, a collision in which a micro black hole may be created.

Gravitational collapse is not the only process that could create black holes. In principle, black holes could be formed in high-energy collisions that achieve sufficient density. As of 2002, no such events have been detected, either directly or indirectly as a deficiency of the mass balance in particle accelerator experiments. This suggests that there must be a lower limit for the mass of black holes. Theoretically, this boundary is expected to lie around the Planck mass (m_P = √ħc/G ≈ 1.2×10¹⁹ GeV/c² ≈ 2.2×10⁻⁸ kg), where quantum effects are expected to invalidate the predictions of general relativity. This would put the creation of black holes firmly out of reach of any high-energy process occurring on or near the Earth. However, certain developments in quantum gravity suggest that the Planck mass could be much lower: some braneworld scenarios for example put the boundary as low as 1 TeV/c². This would make it conceivable for micro black holes to be created in the high-energy collisions that occur when cosmic rays hit the Earth's atmosphere, or possibly in the Large Hadron Collider at CERN. These theories are very speculative, and the creation of black holes in these processes is deemed unlikely by many specialists. Even if micro black holes could be formed, it is expected that they would evaporate in about 10⁻²⁵ seconds, posing no threat to the Earth.

 

Growth:~

Once a black hole has formed, it can continue to grow by absorbing additional matter. Any black hole will continually absorb gas and interstellar dust from its surroundings and omnipresent cosmic background radiation. This is the primary process through which supermassive black holes seem to have grown. A similar process has been suggested for the formation of intermediate-mass black holes found in globular clusters.

Another possibility for black hole growth, is for a black hole to merge with other objects such as stars or even other black holes. Although not necessary for growth, this is thought to have been important, especially for the early development of supermassive black holes, which could have formed from the coagulation of many smaller objects. The process has also been proposed as the origin of some intermediate-mass black holes.

 

Evaporation:~

In 1974, Hawking predicted that black holes are not entirely black but emit small amounts of thermal radiation; this effect has become known as Hawking radiation. By applying quantum field theory to a static black hole background, he determined that a black hole should emit particles that display a perfect black body spectrum. Since Hawking's publication, many others have verified the result through various approaches. If Hawking's theory of black hole radiation is correct, then black holes are expected to shrink and evaporate over time as they lose mass by the emission of photons and other particles. The temperature of this thermal spectrum (Hawking temperature) is proportional to the surface gravity of the black hole, which, for a Schwarzschild black hole, is inversely proportional to the mass. Hence, large black holes emit less radiation than small black holes.

A stellar black hole of 1 M_☉ has a Hawking temperature of about 100 nanokelvins. This is far less than the 2.7 K temperature of the cosmic microwave background radiation. Stellar-mass or larger black holes receive more mass from the cosmic microwave background than they emit through Hawking radiation and thus will grow instead of shrink. To have a Hawking temperature larger than 2.7 K (and be able to evaporate), a black hole would need a mass less than the Moon. Such a black hole would have a diameter of less than a tenth of a millimeter.

If a black hole is very small, the radiation effects are expected to become very strong. Even a black hole that is heavy compared to a human would evaporate in an instant. A black hole with the mass of a car would have a diameter of about 10⁻²⁴ m and take a nanosecond to evaporate, during which time it would briefly have a luminosity of more than 200 times that of the Sun. Lower-mass black holes are expected to evaporate even faster; for example, a black hole of mass 1 TeV/c² would take less than 10⁻⁸⁸ seconds to evaporate completely. For such a small black hole, quantum gravitation effects are expected to play an important role and could hypothetically make such a small black hole stable, although current developments in quantum gravity do not indicate so.

The Hawking radiation for an astrophysical black hole is predicted to be very weak and would thus be exceedingly difficult to detect from Earth. A possible exception, however, is the burst of gamma rays emitted in the last stage of the evaporation of primordial black holes. Searches for such flashes have proven unsuccessful and provide stringent limits on the possibility of existence of low mass primordial black holes. NASA's Fermi Gamma-ray Space Telescope launched in 2008 will continue the search for these flashes.

 

Observational evidence.

Gas cloud ripped apart by black hole at the centre of the Milky Way.

By their very nature, black holes do not directly emit any electromagnetic radiation other than the hypothetical Hawking radiation, so astrophysicists searching for black holes must generally rely on indirect observations. For example, a black hole's existence can sometimes be inferred by observing its gravitational interactions with its surroundings. However, the Event Horizon Telescope (EHT), run by MIT's Haystack Observatory, is an attempt to directly observe the immediate environment of the event horizon of Sagittarius A*, the black hole at the centre of the Milky Way. The first image of the event horizon may appear as early as 2018. The existence of magnetic fields just outside the event horizon of Sagittarius A*, which were predicted by theoretical studies of black holes, was confirmed by the EHT in 2015.